前言

十分钟学会设计飞翼飞机的要点，主要知识翻译学习于外网。

目标：让有基础的力，力矩，平衡概念的读者也能快速明白和理解如何设计飞翼飞行器

翼形

其实，只要我们选择合适的后掠(sweep)和扭转(twist)设计，那么大部分的翼形都可以作为飞翼和无尾翼布局飞机的翼形。因此，所谓的特有的“飞翼翼形”其实是不存在的。

然而，如果我们想要设计一个具有较宽可操纵范围的无尾翼布局的飞机，那么机翼就应该需要有较小的扭转角（这是为了在整个飞行包线中始终将诱导阻力保持在一个合理的范围内）。在这个条件下，机翼的力矩系数随攻角的变化程度一定不能过大，所以，我们最好采用低力矩系数的翼形。如果是无后掠的情况，那么我们甚至必须要采用具有正力矩系数的翼形，以避免在配平的飞行中需要向上配平襟翼，这种具有正力矩系数的翼形，通常都具有反折型（s型）的中弧线(reflexed camber line)

纵向稳定性

就如同航模飞机他们的天上飞的那些全尺寸的大“堂兄弟”们一样，航模飞机也需要一定的稳定性：即，在飞行中受到小扰动后自动恢复原始状态的能力。至于到底需要多少稳定性，这完全取绝于飞行员的“个人口味”：老鸟喜欢低稳定裕度的飞机，而新手大多喜欢高稳定性裕度的飞机。接下来将介绍如何对于飞翼，我们如何预测重心位置，以及找到合适的后掠和弧度曲线。

无后掠翼设计

对于常规布局飞机，水平尾翼提供了飞机所必需的纵向稳定性。但对于稳定的无后掠翼飞翼飞机，稳定飞机的只能是主翼。在大多数情况下，常常采用反折(s形)弧度线的翼形实现纵向稳定性。

一些重要的气动和机械知识

为了理解为什么反折型翼形提供了纵向稳定性，这两个概念非常重要：

合力和合力矩，C/4点：almostly，AC

作用在机翼各个面上的压力，可以通过一个作用在一个点上的合力和合力矩代替。通常，都将这个点选为四分之一弦长点。当攻角改变时合力将会改变，而合力矩近乎不变（这和c/4点靠经气动中心有关）。攻角增大，合力就会增大。（失速前）
重心：GC点

重心就像飞机的“质心”，飞机的各种转动，都是绕着这个点在动。而飞机的平行移动则是这个点的平移。

平衡性

为什么无尾翼无后掠时要采用（具有正力矩系数的）s型翼形？请看下面的分析。

常规弧形平凸翼形

平衡状态分析：重心在c/4之后，才能静平衡

第一张图：平凸翼形具有”低头“的总力矩（nose heavy moment），为了保持平衡，那么重心必须位于c/4之后，而具体这个距离的远近取绝于低头力矩的大小，也就是说，如果M*=0的话，那么我们需要刚好把重心放到c/4处。(带*表示平衡状态)

静稳定性分析：不能静稳定

第二张图：考虑受到扰动抬头的情况，升力将会增大，然而总力矩几乎不变，因此平衡将被打破，机翼将绕中心顺时针旋转，也就是会”抬头“。这时候，这个系统是静不稳定的，我们就需要引入尾翼来进一步使其具有静稳定性了。

弯折翼型

平衡状态分析：重心在c/4之前，才能静平衡

第一张图：弯折翼形具有”抬头“的总力矩（tail heavy moment），为了保持平衡，那么重心必须位于c/4之前，而具体这个距离的远近取绝于低头力矩的大小，也就是说，如果M*=0的话，那么我们需要刚好把重心放到c/4处。(带*表示平衡状态)

静稳定性分析：可以静稳定

第二张图：考虑受到扰动抬头的情况，升力将会增大，然而总力矩几乎不变，因此平衡将被打破，机翼将绕中心逆时针旋转，也就是会”低头“。这时候，刚好可以自动抵消掉受到扰动导致的抬头，所以这个系统是静稳定的。

气动中心和稳定性

气动中心：攻角改变，但是作用在这个点上的总力矩不变，这个点就是翼形的气动中心。大多数翼形的气动中心都在c/4附近。所以上面的分析中，使用了c/4这个点用来判断，这是因为在实际航模飞行中，c/4点比较好找！如果重心离气动中心远一些，那么飞机的静稳定裕度就越大，静稳定性越强。

后掠翼设计

为了使得飞机在纵向具有一定的静稳定裕度，我们熟知的一个要点是重心(center of gravity, CG)要在气动中心(aerodynamic center, AC)之前。对于飞翼飞机而言，采用后掠翼的一个好处是其能够有效将气动中心后移，从而使得重心能够更方便地配平。

平直翼与后掠翼的对比

气动中心和稳定性

平均气动弦长Cm计算

lu:平均气动弦长；lr：翼根部弦长，λ=lt/lr.梢根比
后掠翼飞翼气动中心的位置

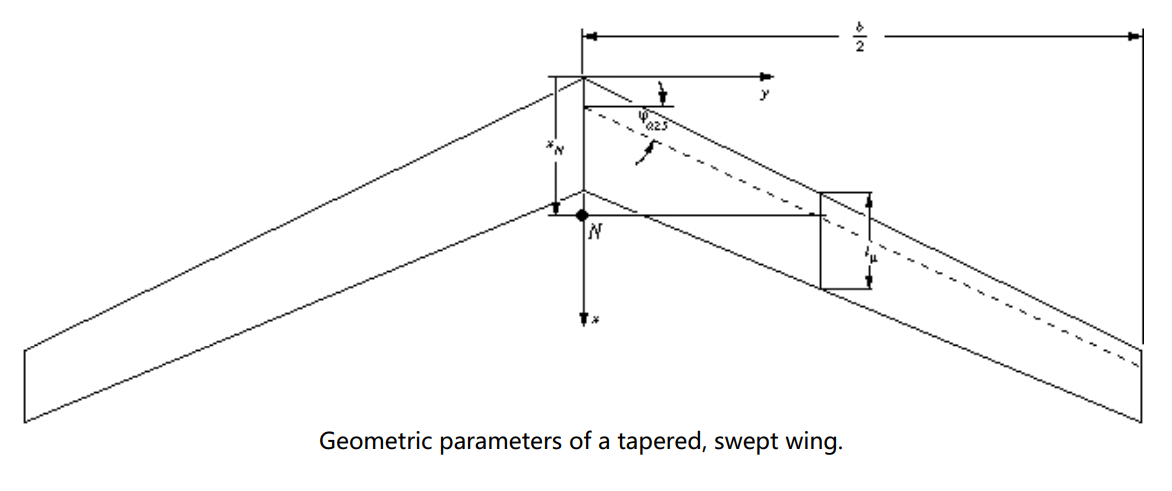
如图，我们能够找到平均气动弦长在机翼上的位置，通过这个位置我们就能够确定气动中心的位置，然后将重心设计到这一点前面即可使得飞机具有静稳定性。

除了以上基于几何关系的方法，我们还能采用下列的经验公式直接估算气动重心的位置。

机翼的扭转（twist）的设计

CG处在AC之前是纵向稳定性的需求，除此之外，为了平衡性，在CG附近的力矩和必须为零。首先因为我们已经确定了确保纵向稳定性的CG位置，我们只能通过调整机翼的扭转使得气动力矩在CG附近的和为零。
在常规布局的飞机上，我们可以通过调整水平尾翼来调整这个力矩，但是在飞翼上我们无法这样做。并且计算这个扭转是十分复杂的
这里参考国外给出的一种估计扭转角的大致方法，这个方法主要借助两张经验图，它可以适用于根部到梢部线性变换的后掠翼。
机翼需要的扭转可以分为两部分：几何扭转和气动扭转
- 几何扭转：翼根和翼梢翼形的x轴的夹角，一般翼尖为负扭转；大的扭转角可以用来稳定具有小后掠角或者高弧度的翼形，但是缺点是当机翼工作在超出设定范围时会增加诱导阻力。
- 气动扭转：翼根和翼尖采用不同的翼形。如果我们选择零升攻角不同的翼形，我们可以减小几何扭转量。这样的话可以减少几何扭转量从而使得机翼的设计性能更好。

计算几何扭转角βreq

我们可以通过两张图表来确定需求的扭转角βreq.

这张表是

根据CL*=1.0，
稳定系数σ*=10%
使用零力矩系数的翼形

得到的标准情况，我们可以将自己的翼形设计的比例叠加上去就能得到我们实际需要的βreq，其中我们可以发现，如果CL=0.5,即缩小50%，那么机翼的扭转也能缩小50%；除此之外，要是我们采用较小的稳定系数，那么也能减少机翼的扭转

零升攻角的变化

如果我们在翼根和翼梢采用不同的翼形，那么他们的零攻角升力方向可能不一样，这将影响平衡状态。通过这种手段，我们可以减少几何扭转

如果翼根，翼梢采用相同的翼形，那么这个角就是0.

翼形力矩系数的影响

翼形的力矩系数对于平衡也有影响，上面这张图可以用来帮助我们找到对扭转角进行修正的合适角度。如果我们采用了具有正力矩系数的翼形，那么β_cm就会为正，那么它将能够减少扭转量。这张图也是根据标准翼形的参考所描绘的，其中cm*=0.05。如果我们在翼根和翼尖采用了不同翼形，那么我们需要利用(c_m,tip+c_m,root)/2来计算这个力矩系数。

最后，我们可以计算出机翼几何扭转角的净值β_geo,即